Se stie ca din numarul 4 se poate obtine orice numar natural n scris in baza zece prin aplicarea urmatoarelor operatii :
Se cere sa se scrie un program care produce un sir de numere construit conform regulilor precedente, sir in care primul numar este 4, iar ultimul este n.
Rez
O prima metoda de abordare a problemei ar fi sa plecam de la 4 si sa incercam sa gasim un sir de transformari ca sa obtinem numarul n. Dar se observa ca la un moment dat putem aplica fie transformarea (1) fie (2), daca numarul este impar. Aceasta ne duce cu gindul la generarea unui arbore de explorare. Metoda este backtracking cu avantajele si dezavantajele ei.
Ideea acestei probleme este de a pleca de la rezultat spre inceput. Adica vom pleca de la numarul n si ii vom aplica operatiile inverse celor definite in enuntul problemei. Ne vom opri in momentul cind vom obtine numarul 4. Afisarea inversa a etapelor va rezolva cerinta problemei.
Aceasta problema contine cerinta de a maximiza numarul de tevi care pot intra intr-o incinta (de exemplu un container).
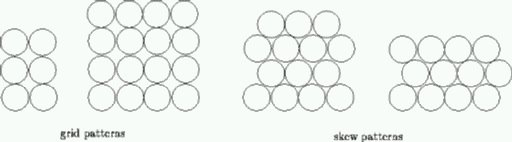
O fabrica produce tevi de diametru constant. Toate tevile sunt transportate in containere cu sectiune rectangulara. Containerele vin insa de dimensiuni diferite. Tevile sunt stocate pe linii intr-un container astfel ca sa nu existe spatiu intre ele (poate ramine spatiu la sfirsitul liniei). Intr-o sectiune rectangulara, tevile sunt depozitate fie in model retea fie in model diagonal.

Cind tevile sunt depozitate intr-un ontainer, poate ramine ceva spatiu in care nu poate intra nici o teava. Astfel de spatii sunt ocupate cu piese din lemn pentru ca in timpul transportului sa nu se miste.
Dindu-se dimensiunile (lungimea, latimea) unei sectiuni rectangulare a unui container, programul trebuie sa afiseze numarul maxim de tevi care se pot introduce si modul in care acestea au fost aranjate. Dimensiunile sunt exprimate in unitati; diametrul unei tevi este egal cu unitatea. Numarul de tevi este un numar intreg.
3 3 2.9 10 2.9 10.5 11 11
9 retea 29 diagonal 30 diagonal 126 diagonal
Rez